Fibonacci - La Sezione Aurea

Teoria sul Disegno
di Matthew Bates
Al liceo la mia materia preferita non era la matematica. Ho sofferto molto per capire anche le cose basiche, a parte una lezione dove abbiamo studiato le serie di numeri. Per qualche motivo mi trovavo bene, forse perché i numeri in serie mi sembravano un buon uso della matematica. Dopo il liceo sono passato all'università per studiare arte e mi sembrava di aver chiuso con la matematica per sempre. Scoprii di aver sbagliato. L'arte e la matematica sono collegati sopratutto perché si usa la matematica per progettare la nostra realtà e l'arte per rappresentarla. Entrambi ci aiutano a definire il nostro mondo. Gli artisti usano la matematica anche se non vogliono. Per iniziare un dipinto devo pensare alle sue dimensioni. La maggior parte dei quadri sono rettangolari, con una larghezza e un'altezza. Vedete, stiamo usando la matematica prima di iniziare a dipingere! Allora, bisogna decidere quale dimensioni usare per iniziare un dipinto. Trovare le dimensioni giuste è fondamentale perché l'intera opera sarà contenuta all'interno di questo rettangolo. Come influenzerà il rettangolo l'intera opera d'arte? Funzionerà il soggetto dentro lo spazio scelto? Ogni quadro è una finestra, una finestra che guarda dentro l'anima dell'artista. Ogni dipinto ha un significato, diventerà iconico e assumerà una vita propria, sopratutto quando l'opera d'arte sarà esposta al pubblico. Allora si capisce perché è fondamentale la scelta del rettangolo dell’artista per il proprio dipinto. La tela appena assemblata è bianca e candida, la sua unica dimensione è il rettangolo. Questo cambierà, dipingendo il soggetto diventerà visibile, aggiungendo una terza dimensione alla tela. Questa è la magia dell'arte, l'artista trasmette qualcosa dentro la tela e vediamo qualcosa che non c'era prima. Ciò significa che l'artista dovrebbe capire i fondamenti di base della realtà prima di tentare di aggiungere la terza dimensione alla tela. Ora ci accingiamo a tornare alla matematica. Al mio modesto tentativo di capire il mondo intorno a me mi sono imbattuto in una teoria che sembrava improbabile, alla fine molto elegante. E' la teoria che l'intero universo si basa su una serie di numeri conosciuta come la serie di Fibonacci o la sezione aurea.
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597.......................................
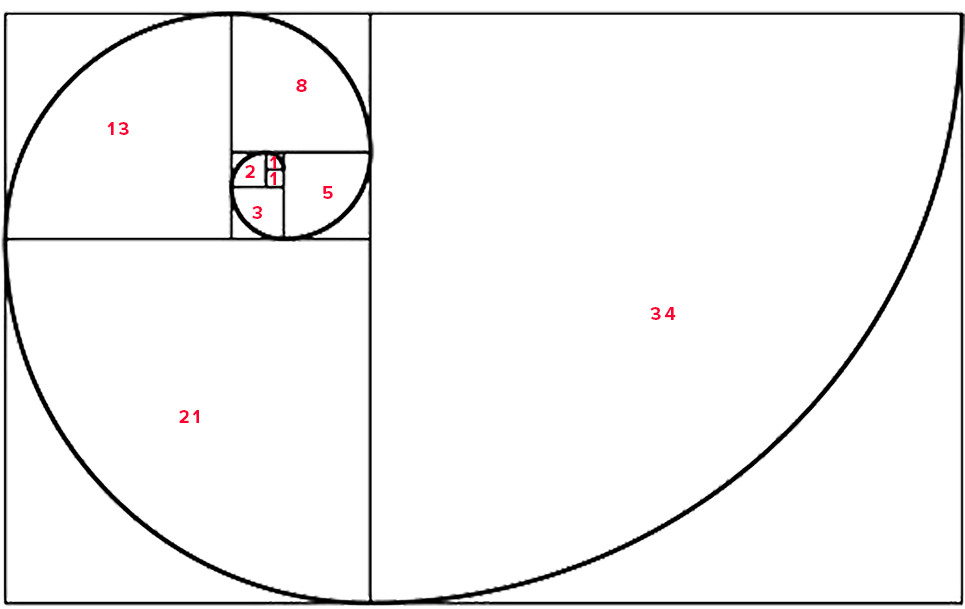
Si inizia con nulla, lo zero e poi, magicamente, si aggiunge uno, aumentando del 100% le quantità delle cose che esistono. Visto che hai solo uno, bisogna aggiungere un altro magico uno per proseguire. Ora hai due. Questa è la parte della sequenza che mi ha sempre incuriosito, sopratutto perché è così lontana dal resto della serie. Abbiamo lo zero, due da uno e due. Non molto con cui giocare. Ora che abbiamo uno e due è naturale aggiungerli insieme per ottenere tre. Due e tre sono molto più interessanti, sopratutto per l'artista che sta cercando di mettere insieme un rettangolo per iniziare un quadro. Così tre più due fa cinque, tre più cinque fa otto e così via, all'infinito. E allora? Beh, la cosa è così elegante da sfidare il pensiero razionale. Dopo pochi passi nella serie di Fibonacci, due numeri, purché siano uno accanto all’altro, si possono dividere. Per esempio: prendiamo 610 diviso per 987, il risultato di 0,618034448......un numero irrazionale come pi greco. Ciò che è sorprendente è che se si prende il numero successivo nella serie, 1597 e si divide per 987, si ottiene 1,61803448......Quindi non importa da quale parte si dividono i numeri, sia il primo numero diviso per il secondo o viceversa, si ottiene sempre la stessa risposta incredibile, conosciuta come la sezione aurea. Tutto questo è interessante, ma si potrebbe dire, "bella coincidenza" un trucco della matematica per intenditori. Non è così semplice. Ho scoperto che i sistemi, naturali e non, tendono a migrare verso la sequenza di Fibonacci. In natura possiamo vedere che molti essere viventi usano la sequenza di Fibonacci mentre crescono. I più evidenti sono i fiori del girasole, i gusci del Nautilus, fino alla formazione di galassie lontane. Troverete molte informazioni su internet di queste proprietà, quindi non vi annoierò a morte elencandole, se siete nuovi a quest’argomento, fate un giro su Google, Io vorrei parlare di qualcos'altro. Io penso che la sequenza di Fibonacci che crea la sezione aurea è una forma pura di disegno. Ho scoperto che la sequenza di Fibonacci può essere utilizzata per ottenere un’ immagine chiara, che sia bella da vedere, quindi, degna del mio tempo come artista. Ho basato questa teoria su numerosi tentativi durante la mia vita. Come posso usare la sezione aurea nei miei progetti? Semplice, uso i numeri, in sequenza della serie di Fibonacci nel rettangolo del mio quadro. Non c’è bisogno di esser rigidi su come si usano i numeri. Ci potrebbe essere una combinazione di rettangoli all’interno della tela. Utilizzando i numeri di Fibonacci nel disegno del rettangolo, metto l’opera d’arte dentro la sezione aurea. Per dimostrare come funziona la sezione aurea, ho disegnato una griglia che crea la spirale aurea. Inserendo i numeri della serie di Fibonacci all’interno di una scatola quadrata, che ha le dimensioni di ciascun numero, è possibile creare la spirale aurea. La successiva casella numerata si basa sulla somma delle due scatole più piccole accanto ad essa e così cresce esponenzialmente.
Ecco la griglia:
Ecco alcuni esempi dei quadri che ho creato con la griglia di Fibonacci sovrapposta sopra ciascun dipinto:
“Ponte degli Innamorati di Verona” ha le dimensioni di 180cm x 80cm. Suddividendo la lunghezza in due parti otteniamo 50cm + 130cm. Così troviamo tre numeri di Fibonacci consecutivi, 5,8,13. In questo modo il disegno complessivo del ponte si inserisce naturalmente dentro la spirale di Fibonacci. Otteniamo due rettangoli Fibonacci sui lati del quadro e un quadrato di 80cm x 80cm nel mezzo tra i due rettangoli Fibonacci nei lati del dipinto.

“Entrando nel Duomo” dimostra l’utilizzo di più griglie di Fibonacci in un dipinto.
“Piazza Santo Spirito” ha le stesse dimensioni del dipinto accanto e usa le stesse griglie di Fibonacci usando un altro punto di vista.

“Giaggiolo Giallo” utilizza la griglia di Fibonacci nelle sue dimensioni esterne.
“Via del Corso” ha la griglia di Fibonacci nelle sue dimensioni esterne e mostra nei quadrati rossi che c’è un’ ulteriore visione della serie di Fibonacci andando indietro, creando una specie di visione 3d.
Io vivo a Firenze da oltre vent’anni. Firenze è bella e mi offre una quantità infinita di ispirazioni. Ogni volta che lascio Firenze, succede qualcosa. Di solito, “le fonti” di ispirazione non funzionano bene. Difficilmente trovo soggetti al di fuori di Firenze degni della mia attenzione e devo aspettare il mio rientro a Firenze per ritrovare di nuovo la mia ispirazione. Spesso mi sono chiesto, “ Ma questa città ha qualcosa di speciale? Ovviamente c’è una storia millenaria e l’arte, anche 500 anni dopo la sua produzione facciamo la fila per ammirarla. Ma c’è di più? Guardando Firenze dall’alto si vede che è un posto straordinario.
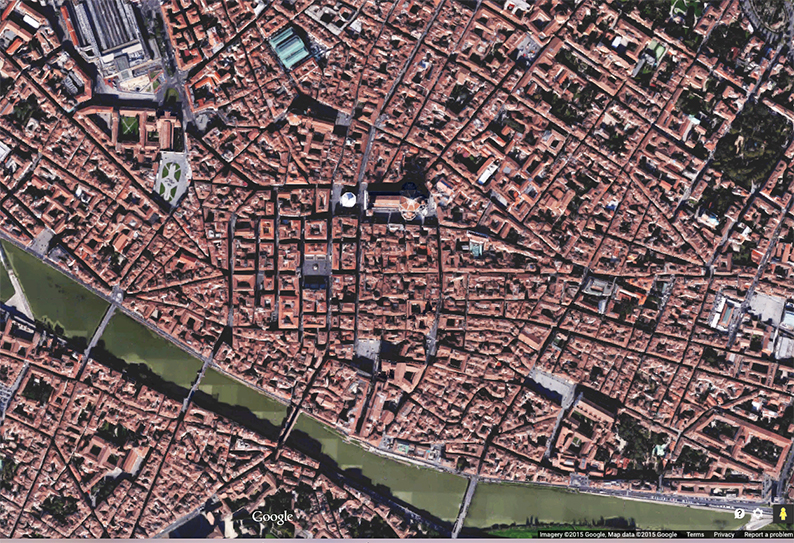
Bella Firenze vista dall'alto
La città ha le sue origine in epoca Romana. Il primo avamposto è stato presumibilmente costruito dentro i confini di quella che oggi si chiama Piazza della Repubblica, che ha una forma rettangolare. Ho pensato, visto che la città si è formata da questo quadrato, cosa succederebbe se metto la griglia di Fibonacci sopra la città usando Piazza della Repubblica nella casella numero uno? E’ accaduto qualcosa di straordinario. La griglia si adatta alla forma del centro storico! La città di Firenze ha preso la forma della sequenza di Fibonacci. E’ stata progettata così? Non penso, perché la città è troppo vecchia e ci sono stati molti cambiamenti strutturali durante la sua storia. Io penso che data la lunghezza della sua permanenza, Firenze ha preso la forma della sequenza di Fibonacci naturalmente. Come altri sistemi complessi, notati prima, tendono a prendere la forma a spirale nelle sue dimensioni.
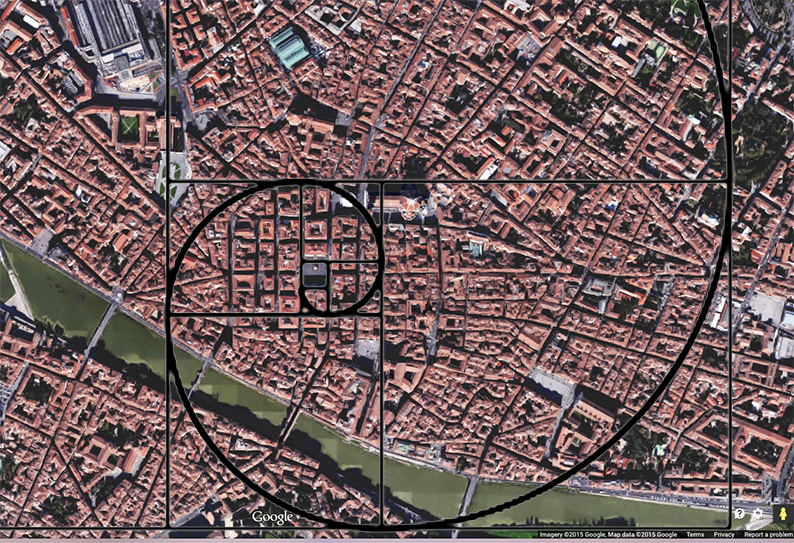
Mettendo la griglia di Fibonacci sopra la città partendo da Piazza della Repubblica, c'entra esattmente
E’ per questo motivo che Io e tantissimi altri trovano ispirazione divina a Firenze? Restando dentro il centro storico di Firenze, che ha preso la forma della sezione aurea, sentiamo un’energia, una forza che definirei creativa, per aiutarci a creare un’arte superiore? Io credo di si! Esattamente come Io metto i miei disegni dentro la griglia di Fibonacci, quando Io stesso sono dentro il centro storico di Firenze, succede la stessa magia. Questa forma pura, la sezione aurea, potrebbe essere la risposta alla nostra ricerca di pace e armonia. A me ha offerto uno strumento utile per creare arte e per trovare l’illuminazione.
Firenze, Matthew Holden Bates
![]()
©2015, Matthew Holden Bates, Firenze, All Rights Reserved
Official Website of Matthew Holden Bates
www.mattbates.net


